Несобственные интегралы определение и их признаки сходимости. Как вычислить несобственный интеграл и выяснить его сходимость. Несобственные интегралы с бесконечным верхним пределом
Примеры исследования несобственных интегралов на сходимость
Пример 1
 .
.
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2
Исследовать на сходимость . Вычислим интеграл по определению:  .
.
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3
Исследовать на сходимость ![]() .
.
<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
 .
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: (т. к. n>0), а интеграл сходится при m>-1 (пример 2). Аналогично, для интеграла I2:
А интеграл сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость .
Подынтегральная функция может быть бесконечно большой (если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу , который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
![]() т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость .
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
![]() .
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
![]() При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
Т. е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость .
Проведем замену переменной: t = lnx, и получим
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения ![]() и a=(1-p)/2.).
и a=(1-p)/2.).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что ![]() При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T
-
Q
E
(1-
P
)
T
³ M=const>0. Тогда для интеграла I2 справедлива оценка
При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T
-
Q
E
(1-
P
)
T
³ M=const>0. Тогда для интеграла I2 справедлива оценка
 ,
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость .
Разобьем исходный интеграл на два:
 .
.
Сходимость.
Интеграл I1 эквивалентен  , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
, т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
 .
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
 , при p>0.
, при p>0.
Таким образом, интеграл сходится при 0 Абсолютная сходимость
Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху: Для доказательства расходимости при p£1 оценим интеграл снизу Разобьем последний интеграл от разности функций на разность интегралов Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится - то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев. Расходится (пример 1) при p<1. сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл оценивается снизу расходящимся интегралом, т. е. расходится. Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл расходится. Таким образом, исходный интеграл сходится абсолютно при 0 Если подинтегральная функция имеет на (конечном) интервале интегрирования разрыв второго рода, говорят о несобственном интеграле второго рода. Обозначим интервал интегрирования $\left[ a, \, b \right ]$, оба этих числа ниже полагаются конечными. Если имеется всего 1 разрыв, он может находиться или в точке $a$, или в точке $b$, или внутри интервала $(a,\,b)$. Рассмотрим сначала случай, когда разрыв второго рода имеется в точке $a$, а в остальных точках подинтегральная функция непрерывна. Итак, мы обсуждаем интеграл
\begin{equation}
I=\int _a^b f(x)\,dx, (22)
\label{intr2}
\end{equation}
причем $f(x) \rightarrow \infty $, когда $x \rightarrow a+0$. Как и ранее, прежде всего следует придать смысл этому выражению. Для этого рассмотрим интеграл
\[
I(\epsilon)=\int _{a+\epsilon}^b f(x)\,dx.
\]
Определение.
Пусть существует конечный предел
\[
A=\lim _{\epsilon \rightarrow +0}I(\epsilon)=\lim _{\epsilon \rightarrow +0}\int _{a+\epsilon}^b f(x)\,dx.
\]
Тогда говорят, что несобственный интеграл второго рода (22) сходится, и ему приписывают значение $A$, саму функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$. Рассмотрим интеграл
\[
I=\int ^1_0\frac{dx}{\sqrt{x}}.
\]
Подинтегральная функция $1/\sqrt{x}$ при $x \rightarrow +0$ имеет бесконечный предел, так что в точке $x=0$ она имеет разрыв второго рода. Положим
\[
I(\epsilon)=\int ^1_{\epsilon }\frac{dx}{\sqrt{x}}\,.
\]
В данном случае первообразная известна,
\[
I(\epsilon)=\int ^1_{\epsilon }\frac{dx}{\sqrt{x}}=2\sqrt{x}|^1_{\epsilon }=2(1-\sqrt{\epsilon })\rightarrow 2
\]
при $\epsilon \rightarrow +0$. Таким образом, исходный интеграл является сходящимся несобственным интегралом второго рода, причем он равен 2. Рассмотрим вариант, когда разрыв второго рода подинтегральной функции имеется на верхнем пределе интервала интегрирования. Этот случай можно свести к предыдущему, сделав замену переменной $x=-t$ и затем переставив пределы интегрирования. Рассмотрим вариант, когда разрыв второго рода у подинтегральной функции имеется внутри интервала интегрирования, в точке $c \in (a,\,b)$. В данном случае исходный интеграл
\begin{equation}
I=\int _a^bf(x)\,dx (23)
\label{intr3}
\end{equation}
представляют в виде суммы
\[
I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx.
\]
Определение.
Если оба интеграла $I_1, \, I_2$ сходятся, то несобственный интеграл (23) называют сходящимся и ему приписывают значение, равное сумме интегралов $I_1, \, I_2$, функцию $f(x)$ называют интегрируемой на интервале $\left[ a, \, b\right]$. Если хотя бы один из интегралов $I_1,\, I_2$ является расходящимся, несобственный интеграл (23) называют расходящимся. Сходящиеся несобственные интегралы 2 рода обладают всеми стандартными свойствами обычных определенных интегралов. 1.
Если $f(x)$, $g(x)$ интегрируемы на интервале $\left[ a, \,b \right ]$, то их сумма $f(x)+g(x)$ также интегрируема на этом интервале, причем
\[
\int _a^{b}\left(f(x)+g(x)\right)dx=\int _a^{b}f(x)dx+\int _a^{b}g(x)dx.
\]
2.
Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любой константы $C$ функция $C\cdot f(x)$ также интегрируема на этом интервале, причем
\[
\int _a^{b}C\cdot f(x)dx=C \cdot \int _a^{b}f(x)dx.
\]
3.
Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, причем на этом интервале $f(x)>0$, то
\[
\int _a^{b} f(x)dx\,>\,0.
\]
4.
Если $f(x)$ интегрируема на интервале $\left[ a, \, b \right ]$, то для любого $c\in (a, \,b)$ интегралы
\[
\int _a^{c} f(x)dx, \quad \int _c^{b} f(x)dx
\]
тоже сходятся, причем
\[
\int _a^{b}f(x)dx=\int _a^{c} f(x)dx+\int _c^{b} f(x)dx
\]
(аддитивность интеграла по интервалу).
Рассмотрим интеграл
\begin{equation}
I=\int _0^{1}\frac{1}{x^k}\,dx. (24)
\label{mod2}
\end{equation}
Если $k>0$, подинтегральная функция стремится к $\infty$ при $x \rightarrow +0$, так что интеграл - несобственный второго рода. Введем функцию
\[
I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx.
\]
В данном случае первообразная известна, так что
\[
I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x^k}\,dx\,=\frac{x^{1-k}}{1-k}|_{\epsilon}^1= \frac{1}{1-k}-\frac{\epsilon ^{1-k}}{1-k}.
\]
при $k \neq 1$,
\[
I(\epsilon)=\int _{\epsilon}^{1}\frac{1}{x}\,dx\,=lnx|_{\epsilon}^1= -ln \epsilon.
\]
при $k = 1$. Рассматривая поведение при $\epsilon \rightarrow +0$, приходим к выводу, что интеграл (20) сходится при $k Теорема
(первый признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны при $x\in (a,\,b)$, причем $0
1.
Если интеграл
\[
\int _a^{b}g(x)dx
\]
сходится, то сходится и интеграл
\[
\int _a^{b}f(x)dx.
\]
2.
Если интеграл
\[
\int _a^{b}f(x)dx
\]
расходится, то расходится и интеграл
\[
\int _a^{b}g(x)dx.
\] Теорема
(второй признак сравнения). Пусть $f(x)$, $g(x)$ - непрерывны и положительны при $x\in (a,\,b)$, причем существует конечный предел
\[
\theta = \lim_{x \rightarrow a+0} \frac{f(x)}{g(x)}, \quad \theta \neq 0, \, +\infty.
\]
Тогда интегралы
\[
\int _a^{b}f(x)dx, \quad \int _a^{b}g(x)dx
\]
сходятся или расходятся одновременно. Рассмотрим интеграл
\[
I=\int _0^{1}\frac{1}{x+\sin x}\,dx.
\]
Подинтегральное выражение - положительная функция на интервале интегрирования, подинтегральная функция стремится к $\infty$ при $x \rightarrow +0$, так что наш интеграл - несобственный второго рода. Далее, при $x \rightarrow +0$ имеем: если $g(x)=1/x$, то
\[
\lim _{x \rightarrow +0}\frac{f(x)}{g(x)}=\lim _{x \rightarrow +0}\frac{x}{x+\sin x}=\frac{1}{2} \neq 0,\, \infty \, .
\]
Применяя второй признак сравнения, приходим к выводу, что наш интеграл сходится или расходится одновременно с интегралом
\[
\int _0^{+1}\frac{1}{x}\,dx .
\]
Как было показано в предыдущем примере, этот интеграл расходится ($k=1$). Следовательно, исходный интеграл тоже расходится. Вычислить несобственный интеграл или установить его сходимость (расходимость). 1.
\[
\int _{0}^{1}\frac{dx}{x^3-5x^2}\,.
\]
2.
\[
\int _{3}^{7}\frac{x\,dx}{(x-5)^2}\,.
\]
3.
\[
\int _{0}^{1}\frac{x\,dx}{\sqrt{1-x^2}}\,.
\]
4.
\[
\int _{0}^{1}\frac{x^3\,dx}{1-x^5}\,.
\]
5.
\[
\int _{-3}^{2}\frac{dx}{(x+3)^2}\,.
\]
6.
\[
\int _{1}^{2}\frac{x^2\,dx}{(x-1)\sqrt{x-1}}\,.
\]
7.
\[
\int _{0}^{1}\frac{dx}{\sqrt{x+x^2}}\,.
\]
8.
\[
\int _{0}^{1/4}\frac{dx}{\sqrt{x-x^2}}\,.
\]
9.
\[
\int _{1}^{2}\frac{dx}{xlnx}\,.
\]
10.
\[
\int _{1}^{2}\frac{x^3\,dx}{\sqrt{4-x^2}}\,.
\]
11.
\[
\int _{0}^{\pi /4}\frac{dx}{\sin ^4x}\,.
\]
Как известно, нахождение интеграла может представлять собой достаточно сложную задачу. Было бы большим разочарованием заняться вычислением несобственного интеграла и обнаружить в конце пути, что он расходится. Поэтому представляют интерес методы, позволяющие без серьезных вычислений по одному виду функций сделать заключение о сходимости или расходимости несобственного интеграла. Первая и вторая теоремы сравнения, которые будут рассмотрены ниже, в значительной степени помогают исследовать несобственные интегралы на сходимость. Пусть f(x)?0. Тогда функции являются монотонно возрастающими от переменных t или-д (поскольку берем д>0, -д стремится к нулю слева). Если при возрастании аргументов функции F 1 (t) и F 2 (-д) остаются ограниченными сверху, это означает, что соответствующие несобственные интегралы сходятся. На этом основана первая теорема сравнения для интегралов от неотрицательных функций. Пусть для функции f(x)и g(x) при x?a выполнены условия: Тогда из сходимости интеграла следует сходимость интеграла, а из расходимости интеграла следует расходимость Поскольку 0?f(x)?g(x) и функции непрерывны, то По условию интеграл сходится, т.е. имеет конечную величину. Следовательно, интеграл сходится также. Пусть теперь интеграл расходится. Предположим, что интеграл сходится, но тогда должен сходиться интеграл, что противоречит условию. Наше предположение неверно, интеграл расходится. Теорема сравнения для несобственных интегралов 2-го рода. Пусть для функций f(x) и g(x) на промежутке , неограниченно возрастает при x>+0. Для нее при x>+0 справедливо неравенство <. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также. Теорема сравнения для несобственных интегралов 1-го рода. Пусть для функции f(x) и g(x) на промежутке , а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений.
Так появляются несобственные интегралы. Геометрический смысл несобственного интеграла
выясняется довольно просто.
В случае, когда график функции y
= f
(x
)
находится выше оси Ox
, определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y
= f
(x
)
,
осью абсцисс и ординатами x
= a
, x
= b
.
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями
y
= f
(x
)
(на рисунке ниже - красного цвета), x
= a
и осью абсцисс. Аналогичным образом определяются несобственные интегралы и для других бесконечных
интервалов: Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный
интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный
интеграл называется расходящимся. Использование предела интеграла вместо самого несобственного
интеграла.
Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода. Узнаем об этом сейчас же. Итак, запись несобственного интеграла как
отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен. Определение.
Несобственным интегралом с бесконечным верхним пределом
интегрирования от непрерывной функции f
(x
)
на промежутке
от a
до ∞
называется
предел интеграла этой функции с верхним пределом интегрирования b
и нижним пределом интегрирования a
при условии, что верхний предел
интегрирования неограниченно растёт
, т.е. Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся
, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся
и ему не приписывается никакого значения. Пример 1. Вычислить несобственный интеграл
(если он сходится). Решение. На основании определения несобственного интеграла находим Так как предел существует и равен 1, то и данный несобственный интеграл сходится
и равен 1. В следующем примере подынтегральная функция почти как в примере 1, только степень
икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость.
То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится,
а при каких расходится? Пример 2. Исследовать на сходимость несобственный интеграл
(нижний предел интегрирования больше нуля). Решение. Предположим сначала, что , тогда В полученном выражении перейдём к пределу при : Нетрудно видеть, что предел в правой части существует и равен нулю, когда
, то есть
, и не существует, когда
, то есть
. В первом случае, то есть при
имеет место .
Если , то
Вывод нашего исследования следующий: данный несобственный интеграл
сходится
при и
расходится
при . Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница Это обобщённая формула Ньютона-Лейбница. Пример 3. Вычислить несобственный интеграл
(если он сходится). Предел этого интеграла существует: Второй интеграл, составляющий сумму, выражающую исходный интеграл: Предел этого интеграла также существует: Находим сумму двух интегралов, являющуюся и значением исходного несобственного
интеграла с двумя бесконечными пределами: Пусть функция f
(x
)
задана на
отрезке от a
до b
и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b
,
в то время как во всех остальных точках отрезка она непрерывна. Определение.
Несобственным интегралом функции f
(x
)
на отрезке от a
до b
называется предел интеграла этой функции с верхним пределом интегрирования c
,
если при стремлении c
к b
функция неограниченно возрастает, а в точке x
= b
функция не определена
, т.е. Если этот предел существует, то несобственный интеграл второго рода называется
сходящимся, в противном случае - расходящимся. Используя формулу Ньютона-Лейбница, выводим. , т. е. интеграл сходится при p>1.
, т. е. интеграл сходится при p>1. .
. .
.10.2.1 Определение и основные свойства
10.2.2 Признаки сходимости несобственных интегралов 2 рода
![]()

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
![]() .
.

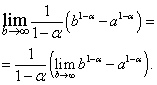
 и
не существует.
и
не существует.![]() ,
можно вывести следующую очень похожую на неё формулу:
,
можно вывести следующую очень похожую на неё формулу: .
.![]()

![]() .
.Несобственные интегралы второго рода - от неограниченных функций и их сходимость
![]() .
.